Example of Creating Aligned Hierarchies for a Mazurka Score
In this example, we will walk through the elements of the repytah package that pertain to the creation of aligned hierarchies for a music-based data stream (eg. a song).
Beginning with features (such as MFCCs and chroma features) for each timestep in your music-based data stream, there are several steps to this process:
Create the self-dissimilarity matrix (SDM).
Highlight pairs of timesteps that are close enough to be considered as repetitions of each other. (In other words, threshold the SDM)
Find pairs of structure repetitions (represented as diagonals within the thresholded SDM).
Find any pairs of structure repetitions not found in step 2, and group the structure repetitions.
Remove any repeated structures that have overlapped instances.
Distill the collection of repeated structures into the essential structure components , i.e. the smallest meaningful repetitions on which all larger repeats are constructed. Each timestep will be contained in no more than one essential structure component
Note: The walk-through of this example is very similar to the code in example.py found in this package.
We begin by importing the necessary packages:
[1]:
# NumPy and SciPy are required for mathematical operations
import scipy.io as sio
import numpy as np
# Pandas is used to import the csv
import pandas as pd
# Import all modules from repytah
from repytah import *
# Matplotlib is used to display outputs
import matplotlib.pyplot as plt
# Make the images clear
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
# Hide code (optional)
import ipywidgets as widgets
from IPython.display import display, HTML
javascript_functions = {False: "hide()", True: "show()"}
button_descriptions = {False: "Show code", True: "Hide code"}
def toggle_code(state):
output_string = "<script>$(\"div.input\").{}</script>"
output_args = (javascript_functions[state],)
output = output_string.format(*output_args)
display(HTML(output))
def button_action(value):
state = value.new
toggle_code(state)
value.owner.description = button_descriptions[state]
state = True
toggle_code(state)
button = widgets.ToggleButton(state, description = button_descriptions[state])
button.observe(button_action, "value")
display(button)
Step 0: Create the SDM
In this phase, there are a few crucial details, namely importing the data file that we would like to unearth hierarchical structural information for and determining the appropriate dissimilarity measure to use. If you already have (symmetrical) matrix representations for your data stream, then you may find it more appropriate to load your matrix and then skip ahead to Step 1 or Step 2.
This step assumes that your music-based data stream (ie. a recording or score) has already had your preferred features extracted (like chroma or MFCCs) and is arranged into columns such that each column represents a time step (or beat). We refer to this as a feature vector matrix as each feature vector is laid out as column within one cohesive matrix.
Importing data for structure analysis
Note: For this demonstration, we are using the load_ex_data() built-in function from the example module to load our data. To recreate our example, you could do the same. This is an optional task and the normal method of reading in a data file will work.
We are using Chopin’s Mazurka Op.6, No.1 as input for this demonstration.
[2]:
# Import csv
file_in = load_ex_data('data/input.csv').to_numpy()
fv_mat = file_in
Creating the SDM
In just one line, we define the self-dissimilarity matrix. This function create_sdm, uses feature vectors to create an audio shingle for each time step and represents these shingles as vectors by stacking the relevant feature vectors on top of each other. Then, the cosine distance is found between these shingles.
[3]:
# Number of feature vectors per shingle
num_fv_per_shingle = 12
# Create the self-dissimilarity matrix
self_dissim_mat = create_sdm(fv_mat, num_fv_per_shingle)
print('self_dissim_mat:\n', self_dissim_mat)
# Produce a visualization
SDM = plt.imshow(self_dissim_mat, cmap="RdBu")
plt.title('Self-Dissimilarity Matrix')
plt.show()
self_dissim_mat:
[[0. 0.36468911 0.58429924 ... 0.57425539 0.77909953 0.82434591]
[0.36468911 0. 0.41660702 ... 0.68829818 0.64039838 0.80480641]
[0.58429924 0.41660702 0. ... 0.72072778 0.59670143 0.57191158]
...
[0.57425539 0.68829818 0.72072778 ... 0. 0.60941866 0.70720396]
[0.77909953 0.64039838 0.59670143 ... 0.60941866 0. 0.39416349]
[0.82434591 0.80480641 0.57191158 ... 0.70720396 0.39416349 0. ]]

Step 1: Threshold the SDM
In this step, the self-dissimilarity matrix is thresholded to produce a binary matrix of the same dimensions. This matrix is used to identify repeated structures, which are represented by diagonals of the same length.
[4]:
song_length = self_dissim_mat.shape[0]
thresh = 0.02
# Threshold the SDM to produce a binary matrix
thresh_dist_mat = (self_dissim_mat <= thresh)
print('thresh_dist_mat:\n', thresh_dist_mat)
# Produce a visualization
SDM = plt.imshow(thresh_dist_mat, cmap="Greys")
plt.title('Thresholded Matrix')
plt.show()
thresh_dist_mat:
[[ True False False ... False False False]
[False True False ... False False False]
[False False True ... False False False]
...
[False False False ... True False False]
[False False False ... False True False]
[False False False ... False False True]]

Step 2: Find the diagonals present and store all pairs of repeats found in a list
The diagonals in the thresholded matrix are found and recorded in an array of repeats. find_initial_repeats does this by looking for the largest repeated structures in thresh_dist_mat, which are illustrated in the above Thresholded Matrix diagram. Once all repeated structures are found, which are represented as diagonals present in thresh_dist_mat, they are stored with their start/end indices and lengths in a list. As each diagonal is found, it is removed to avoid identifying
repeated sub-structures.
Below is the listing of the pairs of repeats found by find_initial_repeats:
[5]:
all_lst = find_initial_repeats(thresh_dist_mat, np.arange(1, song_length + 1), 0)
print('all_lst:\n', all_lst)
all_lst:
[[ 2 2 26 26 1]
[ 2 2 74 74 1]
[ 2 2 146 146 1]
[ 2 2 218 218 1]
[ 2 2 314 314 1]
[ 26 26 50 50 1]
[ 50 50 74 74 1]
[ 50 50 146 146 1]
[ 50 50 218 218 1]
[ 50 50 314 314 1]
[247 250 271 274 4]
[124 156 292 324 33]
[196 228 292 324 33]
[ 2 36 290 324 35]
[ 50 84 290 324 35]
[ 3 38 123 158 36]
[ 51 86 195 230 36]
[ 3 39 195 231 37]
[ 1 38 49 86 38]
[ 51 122 123 194 72]
[ 87 158 159 230 72]
[ 1 325 1 325 325]]
Let’s take moment to examine what we have and time it back to the original thresholded SDM. The first ten pairs listed in all_lst are repeats of length 1. We also note that the last “pair” of repeats is the whole score being matched to itself. For now, we set this “repeat” and the ones that are of length 1 aside.
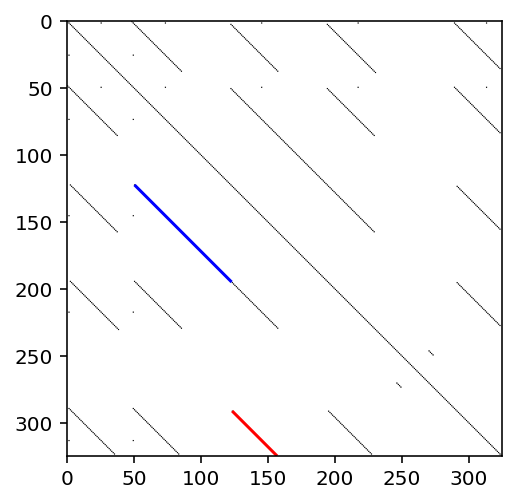
In the image below, for each pair of repeats, we color one of the two diagonals associated to that pairing. The second one is the matching diagonal when flipped over the main diagonal.
For example, the red diagonal represents the pair of repeats that start at beats 124 and 292 and are 33 beats long, and the blue diagonal represents the pair of repeats that start at beat 51 and 123 and are 72 beats long.
[8]:
visualize_all_lst(thresh_dist_mat)
Step 3: Find any diagonals in the thresholded matrix T that are contained in larger diagonals in T but not found in step 2, then group pairs of repeats
Any smaller diagonals that are contained in larger diagonals and are not found in step 2 are found and added to the array of repeats in this step. All possible repeat lengths are looped over in all_lst, and larger repeats containing smaller repeats are broken up into up to 3 sections each, the part before the overlap, the overlap, and the part after the overlap. With this, a more complete list of repeated structures is created.
[9]:
complete_lst = find_complete_list(all_lst, song_length)
print('complete_lst:\n', complete_lst)
complete_lst:
[[ 1 1 49 49 1 1]
[ 2 2 26 26 1 2]
[ 2 2 50 50 1 2]
[ 2 2 74 74 1 2]
[ 2 2 146 146 1 2]
[ 2 2 218 218 1 2]
[ 2 2 290 290 1 2]
[ 2 2 314 314 1 2]
[ 26 26 50 50 1 2]
[ 26 26 74 74 1 2]
[ 26 26 146 146 1 2]
[ 26 26 218 218 1 2]
[ 26 26 314 314 1 2]
[ 50 50 74 74 1 2]
[ 50 50 146 146 1 2]
[ 50 50 218 218 1 2]
[ 50 50 290 290 1 2]
[ 50 50 314 314 1 2]
[ 74 74 146 146 1 2]
[ 74 74 218 218 1 2]
[ 74 74 314 314 1 2]
[146 146 218 218 1 2]
[146 146 314 314 1 2]
[218 218 314 314 1 2]
[ 3 3 123 123 1 3]
[ 3 3 195 195 1 3]
[ 51 51 123 123 1 3]
[ 51 51 195 195 1 3]
[ 39 39 231 231 1 4]
[ 1 2 49 50 2 1]
[ 2 3 290 291 2 2]
[ 50 51 290 291 2 2]
[ 37 38 85 86 2 3]
[ 37 38 157 158 2 3]
[ 85 86 229 230 2 3]
[157 158 229 230 2 3]
[ 37 39 229 231 3 1]
[247 250 271 274 4 1]
[ 27 36 315 324 10 1]
[ 75 84 315 324 10 1]
[147 156 315 324 10 1]
[219 228 315 324 10 1]
[ 27 38 75 86 12 1]
[ 27 38 147 158 12 1]
[ 75 86 219 230 12 1]
[147 158 219 230 12 1]
[ 27 39 219 231 13 1]
[124 145 292 313 22 1]
[196 217 292 313 22 1]
[ 3 25 123 145 23 1]
[ 3 25 195 217 23 1]
[ 51 73 123 145 23 1]
[ 51 73 195 217 23 1]
[ 2 25 290 313 24 1]
[ 50 73 290 313 24 1]
[ 1 25 49 73 25 1]
[ 4 36 124 156 33 1]
[ 4 36 196 228 33 1]
[ 4 36 292 324 33 1]
[ 52 84 124 156 33 1]
[ 52 84 196 228 33 1]
[ 52 84 292 324 33 1]
[124 156 196 228 33 1]
[124 156 292 324 33 1]
[196 228 292 324 33 1]
[ 3 36 291 324 34 1]
[ 51 84 291 324 34 1]
[ 2 36 50 84 35 1]
[ 2 36 290 324 35 1]
[ 50 84 290 324 35 1]
[ 3 38 51 86 36 1]
[ 3 38 123 158 36 1]
[ 3 38 195 230 36 1]
[ 51 86 123 158 36 1]
[ 51 86 195 230 36 1]
[123 158 195 230 36 1]
[ 87 122 159 194 36 2]
[ 3 39 195 231 37 1]
[ 87 123 159 195 37 2]
[ 1 38 49 86 38 1]
[ 85 122 157 194 38 2]
[ 75 122 147 194 48 1]
[ 87 145 159 217 59 1]
[ 51 122 123 194 72 1]
[ 87 158 159 230 72 2]]
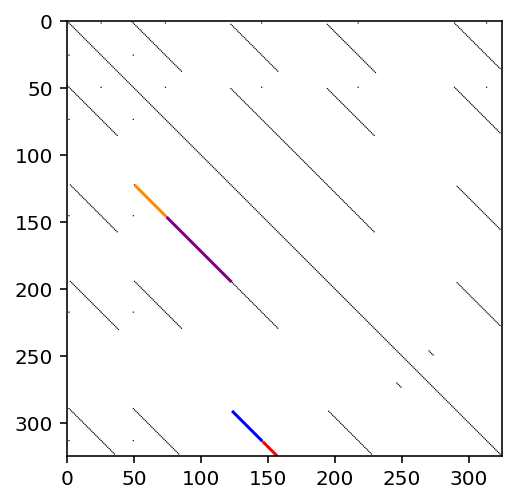
It is clear that complete_list is much longer that all_lst, which makes sense because we are adding smaller pieces of the larger repeats, when an overlap in time has occurred between a smaller repeat and a larger one.
For example, the repeat of length 72 starting at beat 51 overlaps with the smaller repeat of length 48 starting at beat 75 (the purple section).
The image below visualizes the idea of distilling smaller parts from larger repeats in step 2 by showing some of the smaller repetitions found within the larger repeats.
[10]:
visualize_complete_lst(thresh_dist_mat)
Step 4: Remove any repeated structure that has at least two repeats that overlap in time
In this step, repeated structures with the same annotation and length are removed if they are overlapping.
This is done by looping over all possible repeat lengths, finding all the groups of repeats of the same length. For each of those groups, remove_overlaps determines whether there exists any pair of repeats that overlaps in time. If a pair like that exists, all the overlapping repeats are removed.
Along with a list of all the repeats with no overlaps, this step also forms a matrix, a list of the associated lengths of the repeats in the matrix, the annotations of the repeats in the matrix, and a list of the overlaps. The matrix is a binary matrix that visualizes the repeats, representing the start of a repeat with a 1. This matrix, in combination with the list of the lengths of the repeats, can be used to visualize the repeats.
[11]:
output_tuple = remove_overlaps(complete_lst, song_length)
print('List with no overlaps:\n', output_tuple[0])
print('Matrix with no overlaps:\n', output_tuple[1])
print('Lengths of the repeats in the matrix:', output_tuple[2])
print('Annotations of the repeats in the matrix:', output_tuple[3])
print('List of overlaps:\n', output_tuple[4])
List with no overlaps:
[[ 1 1 49 49 1 1]
[ 2 2 26 26 1 2]
[ 2 2 50 50 1 2]
[ 2 2 74 74 1 2]
[ 2 2 146 146 1 2]
[ 2 2 218 218 1 2]
[ 2 2 290 290 1 2]
[ 2 2 314 314 1 2]
[ 3 3 123 123 1 3]
[ 3 3 195 195 1 3]
[ 26 26 50 50 1 2]
[ 26 26 74 74 1 2]
[ 26 26 146 146 1 2]
[ 26 26 218 218 1 2]
[ 26 26 314 314 1 2]
[ 39 39 231 231 1 4]
[ 50 50 74 74 1 2]
[ 50 50 146 146 1 2]
[ 50 50 218 218 1 2]
[ 50 50 290 290 1 2]
[ 50 50 314 314 1 2]
[ 51 51 123 123 1 3]
[ 51 51 195 195 1 3]
[ 74 74 146 146 1 2]
[ 74 74 218 218 1 2]
[ 74 74 314 314 1 2]
[146 146 218 218 1 2]
[146 146 314 314 1 2]
[218 218 314 314 1 2]
[ 1 2 49 50 2 1]
[ 2 3 290 291 2 2]
[ 37 38 85 86 2 3]
[ 37 38 157 158 2 3]
[ 50 51 290 291 2 2]
[ 85 86 229 230 2 3]
[157 158 229 230 2 3]
[ 37 39 229 231 3 1]
[247 250 271 274 4 1]
[ 27 36 315 324 10 1]
[ 75 84 315 324 10 1]
[147 156 315 324 10 1]
[219 228 315 324 10 1]
[ 27 38 75 86 12 1]
[ 27 38 147 158 12 1]
[ 75 86 219 230 12 1]
[147 158 219 230 12 1]
[ 27 39 219 231 13 1]
[124 145 292 313 22 1]
[196 217 292 313 22 1]
[ 3 25 123 145 23 1]
[ 3 25 195 217 23 1]
[ 51 73 123 145 23 1]
[ 51 73 195 217 23 1]
[ 2 25 290 313 24 1]
[ 50 73 290 313 24 1]
[ 1 25 49 73 25 1]
[ 4 36 124 156 33 1]
[ 4 36 196 228 33 1]
[ 4 36 292 324 33 1]
[ 52 84 124 156 33 1]
[ 52 84 196 228 33 1]
[ 52 84 292 324 33 1]
[124 156 196 228 33 1]
[124 156 292 324 33 1]
[196 228 292 324 33 1]
[ 3 36 291 324 34 1]
[ 51 84 291 324 34 1]
[ 2 36 50 84 35 1]
[ 2 36 290 324 35 1]
[ 50 84 290 324 35 1]
[ 3 38 51 86 36 1]
[ 3 38 123 158 36 1]
[ 3 38 195 230 36 1]
[ 51 86 123 158 36 1]
[ 51 86 195 230 36 1]
[ 87 122 159 194 36 2]
[123 158 195 230 36 1]
[ 3 39 195 231 37 1]
[ 87 123 159 195 37 2]
[ 1 38 49 86 38 1]
[ 85 122 157 194 38 2]
[ 75 122 147 194 48 1]
[ 87 145 159 217 59 1]
[ 51 122 123 194 72 1]
[ 87 158 159 230 72 2]]
Matrix with no overlaps:
[[1 0 0 ... 0 0 0]
[0 1 0 ... 0 0 0]
[0 0 1 ... 0 0 0]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
Lengths of the repeats in the matrix: [ 1 1 1 1 2 2 2 3 4 10 12 13 22 23 24 25 33 34 35 36 36 37 37 38
38 48 59 72 72]
Annotations of the repeats in the matrix: [1 2 3 4 1 2 3 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1 1 1 2]
List of overlaps:
[]
Step 5: Find the essential structure components of the song and build the aligned hierarchies
Building the aligned hierarchies takes two final steps: finding the essential structure components and using them to create the full aligned hierarchies. hierarchical_structure first finds the essential structure components with breakup_overlaps_by_intersect. After this, modified versions of steps 2-4 take place to create the full hierarchical structure.
Essential Structure Components
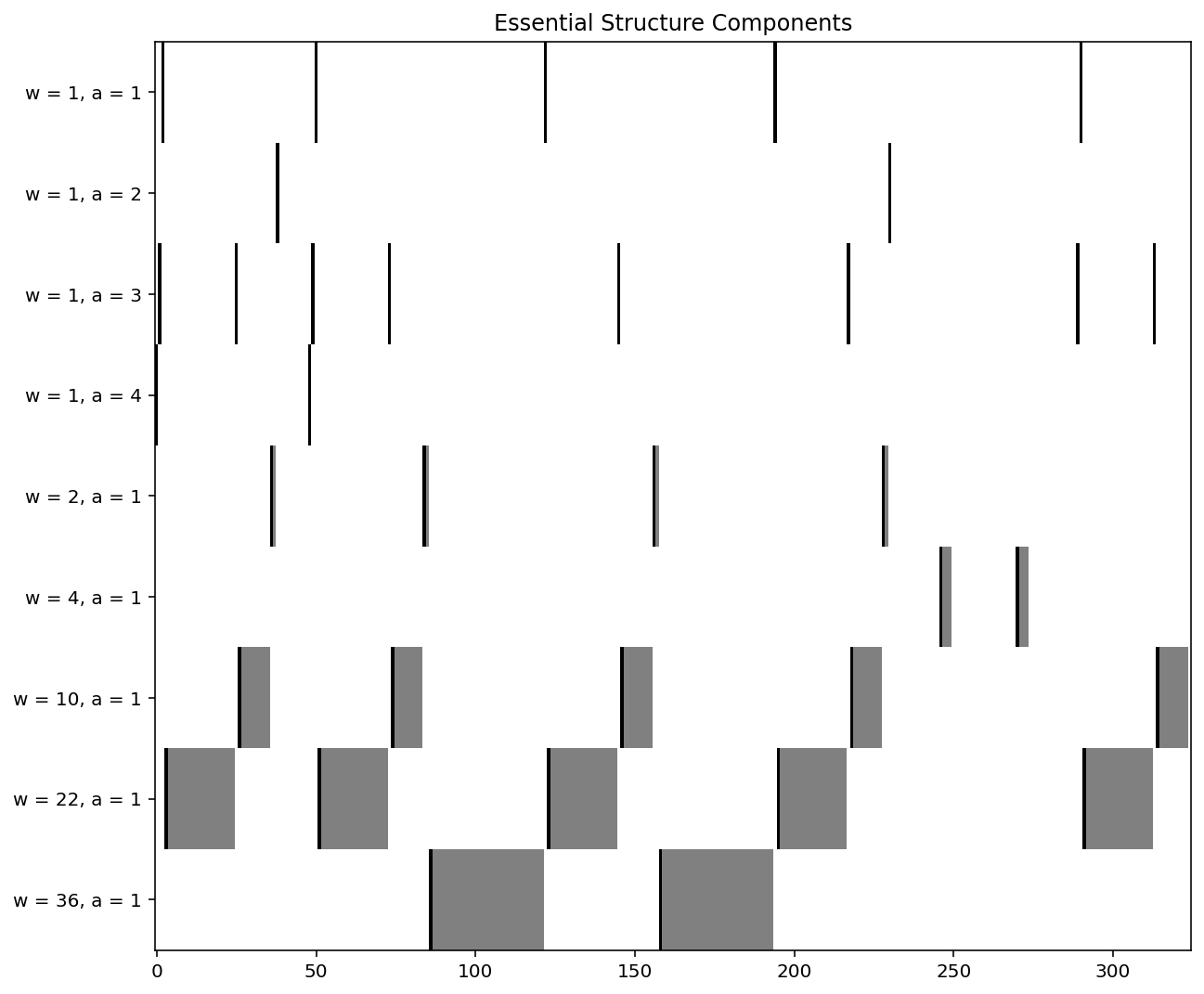
The essential structure components are the structure building blocks; that is they are the smallest meaningful repeated structures. All repeated structures within a piece are constructed with right and left unions of the essential structure components. Each timestep can be in at most one essential structure component. The first panel in the below image shows the essential structure components for our example piece. The visualization is organized such that there is one row per type of repeat. Notice that we have nine types of repeats in the below example.
Creating the aligned hierarchies
After finding the essential structure components for a song, we build the aligned hierarchies using a process whose result is akin to taking right and left unions of the essential structure components. The process begins by creating a list of the essential structure components in the order they appear. We assign each essential structure component the number of the row that it sits in. For consectutive timesteps where there is not essential structure component, we use 0 for that block. In the below example, this list would be: 1,2,3,4,2,5,6,7,0,1,2,3,4,2,5,6,8,3,4,2,5,6,8,3,4,2,5,6,7,0,9,0,9,0,2,3,4,2,5,0.
Using this list, a thresholded dissimilarity matrix is created. Using steps similar to steps two through four above, we can extract information about the combinations of essential structures. From the thresholded dissimilarity matrix, all diagonals are extracted, starting with the longest one, but are not removed. This way, all possible combinations of essential structure components are found. Then, all these combinations are grouped and checked for overlapping repeated combinations. The final product is then restructured to show the widths and annotations for each type of repeated structure (represented by each row).
The figures below represent the final result we get, including two of the most important images: the essential structure components (top most panel) and the complete hierarchical structure (bottom panel).
The figure below with the name Threshold Self-dissimilarity matrix of the ordering Essential Structure Components shows the square thresholded self-dissimilarity matrix such that the (i,j) entry is 1 if the following three conditions are true:
A repeat of an essential structure component is the i-th item in the ordering.
A repeat of an essential structure component is the j-th item in the ordering.
The repeat occurring in the i-th place of the ordering and the one occurring in the j-th place of the ordering are repeats of the same essential structure component.
The figure below with the name Repeated ordered sublists of the Essential Structure Components is the result of extracting all the diagonals and getting pairs of repeated ordered sublists of the essential structure components. The repetitive copies of the same repeat and overlaps are also removed.
The second to last figure labeled Repeated ordered sublists of the Essential Structure Components with leading index highlighted contains the same repeats as Repeated ordered sublists of the Essential Structure Components but only notes the starting item in black and shows the rest of the repeat in gray.
The aligned hierarchies are shown in the last image. This is the result of stretching each essential structure component to its correct length (ie. the one noted in the first image below). This transformation results in a visualization that is the number of time steps of the original song.
[12]:
(mat_no_overlaps, key_no_overlaps) = output_tuple[1:3]
# Distill non-overlapping repeats into essential structure components and
# use them to build the hierarchical representation
output_tuple = hierarchical_structure(mat_no_overlaps, key_no_overlaps, song_length, vis=True)